Penyederhanaan Fungsi Boolean (Tabulasi), Rangkaian Kombinasional

SISDIG_B_TUGAS_3_5113100066

Penyederhanaan Fungsi Boolean (Tabulasi)

            Penyederhanaan fungsi boolean dengan mengggunakan tabulasi merupakan cara ketiga yang dapat dilakukan dalam penyederhanaan suatu fungsi boolean. Dimana dua lainnya ialah dengan cara matematis dan K-map. Ada dua langkah yang harus dilakukan, yaitu: 1.) Tentukanlah semua prime implicants (product terms diperoleh dengan melakukan pengkombinasian secara maksimal terms yang berdekatan). 2.) Menggunakan prime implicants untuk menentukan coverage.

            Ada beberapa ketentuan yang dapat dilakukan untuk penyederhanaan dengan menggunakan tabulasi, yaitu: 1.) Beberapa implicants yang mirip (berdekatan / berbeda 1 digit) digabung menjadi implicant baru. 2.) Penggabungan yang dilakukan harus dilakukan dalam beberapa tahap atau dalam beberapa level. 3.) Perubahan digit pada implicant yang baru ditandandai dengan penulisan ‘-‘.

Contoh :

1010 dan 1011 menjadi 101-

0011 dan 0001 menjadi 00-1

0100 dan 1100 menjadi -100

1101 dan 1001 menjadi 1-01

Contoh Soal :

Sederhanakan fungsi berikut dengan menggunakan cara tabulasi!

Jumlah ‘1’	Minterms	biner
2	m5	0101
	m6	0110
	m12	1100
3	m7	0111
	m14	1110
4	m15	1111

F = (A, B, C, D) = Σ(5, 6, 7, 12, 14, 15)

	w	x	Y	z	F
m0	0	0	0	0	0
m1	0	0	0	1	0
m2	0	0	1	0	0
m3	0	0	1	1	0
m4	0	1	0	0	0
m5	0	1	0	1	1
m6	0	1	1	0	1
m7	0	1	1	1	1
m8	1	0	0	0	0
m9	1	0	0	1	0
m10	1	0	1	0	0
m11	1	0	1	1	0
m12	1	1	0	0	1
m13	1	1	0	1	0
m14	1	1	1	0	1
m15	1	1	1	1	1

Minterms	Biner	2 implicants		4 implicants
m5	0101	m5m7	01-1*
m6	0110	m6m7	011-	m6m7m14m15	-11-*
		m6m14	-110
m7	0111	m7m15	-111
m12	1100	m12m14	11-0*
m14	1110	m14m15	111-

		5	6	7	12	14	15
m5m7	01-1	x		x
m6m7	011-		X	x
m6m14	-110		X			x
m7m15	-111			x			x
m12m14	11-0				x	x
m14m15	111-					x	x
m6m7m14m15	-11-		x	x		x	x

F = BC + A’BD + ABD’

Rangkaian Kombinasional

            Terdapat dua tipe rangkaian logika, yaitu : 1.) Rangkaian Kombinasional (Output hanya ditentukan oleh kombinasi input saat ini). 2.) Rangkaian Sekuensial (Output ditentukan kombinasi input saat ini dan state saat ini dari media penyimoanan(storage), State saat ini dari media penyimpan ditentukan oleh input sebelumnya dan / state sebelumnya).

            Prosedur desain rangkain kombinasional: 1.) Hal pertama yang hasrus dilakukan adalah menentukan jumlah input, jumlah output, dan simbolnya. 2.) Kemudian buatlah tabel kebenaran dan tentukanlah hubungan antara input dan output. 3.) Sederhanakan funsi boolean yang diperoleh dari output sebagai fungsi variabel input. 4.) Lalu, gambarkanlah diagram logikanya. 5.) Untuk tahap terakhir, periksalah kebenaran dari rangkaian yang telah dibuat.

*Untuk kasus tertentu, pertimbangan dalam menentukan desain juga meliputi: jumlah gerbang, jumlah input dari suatu gerbang, waktu yang diperlukan untuk memproses input menjadi output dan jenis gerbang yang tersedia.

Binary Adder – Subtractor

            Dibagi menjadi beberapa jenis:

1.)    Half Adder

Rangkaian kombinasional yang melakukan penjumlahan 2 bit (terdiri dari 2 input dan 2 output).

       c = carry, s = sum

c = xy

s = x’y + xy’

atau

c = xy

s = x Å y

  

2.)    Full Adder

Rangkain Kombinasional yang melakukan penjumlahan 3 bit (terdiri dari 3 input dan 2 output). Dapat dibentuk oleh 2 buah half adder.

Digambarkan sebagai:

 

 

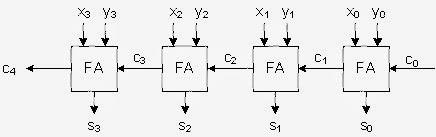
3.)    Binary Adder

n bit binary adder dibentuk oleh n  buah full adder.

Penjumlahan antara x=x₃x₂x₁x₀ dan y=y₃y₂y₁y₀ menggunakan 4 full adder (FA) menghasilkan c₄s₃s₂s₁s_0.

 

4.)    Binary Adder – Subtractor

Binary adder untuk melakukan operasi pengurangan dengan cara menambahkan komplemen bilangan pengurangnya.

Input: x=x₃x₂x₁x₀ dan y=y₃y₂y₁y₀ , output: c₄s₃s₂s₁s_0, m=0 untuk penjumlahan (adder) dan m=1 untuk pengurangan (subtractor).

 

5.)    Decimal Adder

Penjumlahan dari 2 digit desimal kode BCD (A₃A₂A₁A₀ + B₃B₂B₁B₀)

–     Penjumlahan 2 digit dan 1 digit carry menghasilkan output tidak lebih dari: 9 + 9 + 1 = 19                                   

–     Input: 4 bit hasil penjumlahan biner (a,b,c,d) dan 1 bit carry (k)

–     Output: 4 bit hasil konversi ke kode BCD (w,x,y,z) dan 1 bit carry (p)

  c = c = k + ab + ac